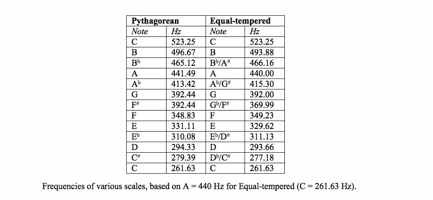
Equal temperament, in music, a tuning system in which the octave is divided into 12 semitones of equal size. Because it enables keyboard instruments to play in all keys with minimal flaws in intonation, equal temperament replaced earlier tuning systems that were based on acoustically pure intervals, that is, intervals that occur naturally in the overtone series. For a more technical explanation of overtones, see sound: Standing waves (Equal Temperament, 2013).

The search for satisfactory tuning systems parallels the development of the Western tonal system, with its reliance on enharmonic equivalence (for example, having the notes F♯ and Gb sound the same) and multiple major and minor keys. In 1581 the Florentine music theorist Vincenzo Galilei (father of the astronomer Galileo) proposed a system of equal intervals for tuning the lute. The Chinese prince and musicologist Zhu Zaiyu in 1596 and the French philosopher and mathematician Marin Mersenne in 1636, among others, wrote of such a system. The idea of equal temperament had its most effective advocates among German musicians and theorists, beginning with Andreas Werckmeister in the early 18th century. Even before the system was widespread, equal temperament was approximated in various degrees as a practical matter, in the small adjustments made by organ tuners and harpsichordists. Equal temperament tuning was widely adopted in France and Germany by the late 18th century and in England by the 19th. Other systems are discussed in tuning and temperament (Equal Temperament, 2013).

In equal temperament, each semitone is measured at 100 cents (1 cent = 1/1200 octave); measuring by frequency (vibrational cycles per second), each semitone step increases in frequency by a factor of the 12th root of 2, or about 1.059 hertz (cycles per second). The 12th semitone, which completes the octave, therefore has a multiplier of 2; for example, the standard A measures 440 hertz, the octave below 220 hertz, and the octave above 880 hertz. Because equal-tempered tuning is calculated by subdividing the octave, it is called a “divisional” system. Earlier European tuning systems—such as meantone temperament and just intonation—were “cyclic” systems, in which given intervals were calculated by adding together other “pure” intervals. Such systems accumulate intonational differences as they move to more distantly related keys (those with increasing numbers of sharps or flats in the key signature), with the result that keyboard instruments and others with fixed intonation will sound unpleasantly out of tune in those keys. In other words, music that would sound perfectly in tune in C major (with no sharps or flats) would sound wrong if transposed to B major (five sharps) because all of the intervals would actually be different in the two keys. In equal temperament, the perfect fifth, such as C–G, is narrower than the natural, or Pythagorean, fifth by 2 cents, a nearly imperceptible amount. These small intonational defects are equally distributed among the 12 tones of the chromatic scale, and only the octave remains as an acoustically pure interval (Equal Temperament, 2013).

The Pythagorean system is so named because it was actually discussed by Pythagoras, the famous Greek mathematician and philosopher, who in the sixth century B.C. already recognized the simple arithmetical relationship involved in intervals of octaves, fifths, and fourths. He and his followers believed that numbers were the ruling principle of the universe, and that musical harmonies were a basic expression of the mathematical laws of the universe. Their model of the universe involved the "celestial spheres" creating a kind of harmony as they moved in circles dictated by the same arithmetical relationships as musical harmonies (Tuning Systems, 2013).

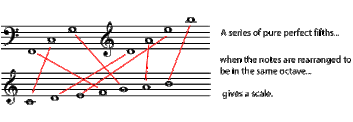
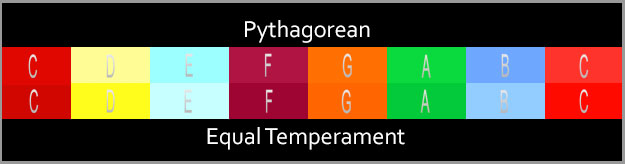
In the Pythagorean system, all tuning is based on the interval of the pure fifth. Pure intervals are the ones found in the harmonic series, with very simple frequency ratios. So a pure fifth will have a frequency ratio of exactly 3:2. Using a series of perfect fifths (and assuming perfect octaves, too, so that you are filling in every octave as you go), you can eventually fill in an entire chromatic scale.
Figure 2: You can continue this series of perfect fifths to get the rest of the notes of a chromatic scale; the series would continue F sharp, C sharp, and so on.

Pythagorean Intonation (Tuning Systems, 2013).

(Tuning Systems, 2013).
The main weakness of the Pythagorean system is that a series of pure perfect fifths will never take you to a note that is a pure octave above the note you started on. To see why this is a problem, imagine beginning on a C. A series of perfect fifths would give: C, G, D, A, E, B, F sharp, C sharp, G sharp, D sharp, A sharp, E sharp, and B sharp. In equal temperament (which doesn't use pure fifths), that B sharp would be exactly the same pitch as the C seven octaves above where you started (so that the series can, in essence, be turned into a closed loop, the Circle of Fifths). Unfortunately, the B sharp that you arrive at after a series of pure fifths is a little higher than that C.

So in order to keep pure octaves, instruments that use Pythagorean tuning have to use eleven pure fifths and one smaller fifth. The smaller fifth has traditionally been called a wolf fifth because of its unpleasant sound. Keys that avoid the wolf fifth sound just fine on instruments that are tuned this way, but keys in which the wolf fifth is often heard become a problem. To avoid some of the harshness of the wolf intervals, some harpsichords and other keyboard instruments were built with split keys for D sharp/E flat and for G sharp/A flat. The front half of the key would play one note, and the back half the other (differently tuned) note (Tuning Systems, 2013).

Pythagorean tuning was widely used in medieval and Renaissance times. Major seconds and thirds are larger in Pythagorean intonation than in equal temperament, and minor seconds and thirds are smaller. Some people feel that using such intervals in medieval music is not only more authentic, but sounds better too, since the music was composed for this tuning system (Tuning Systems, 2013).
           

This project’s goal is not to standardize Alexander Scriabin’s colors to existing tuning systems.  The purpose of this project is to create a study to coordinate colors in our day-to-day surroundings as a reflection of sounds.  Students and teachers can come up with their own set of colors, and then assign them to their desired order to create music as well as tuning exercises by brightening or darkening the color to reflect a sharp or flat tone, respectively.  Equal temperament as the standard principle rather than the Pythagorean system, which—as can be seen above—have a slightly flat 3rd and 7th to modern ears. The precise mathematical system is more reliable as a foundation, and is the one used now in all Western music.

Pythagorean
Note: C D E F G A B C
Cents: (C-204) (D-204) (E-90) (F-204) (G-204) (A-204) (B-90) (C-204)

Note: C D E F G A B C
Cents: (C-200) (D-200) (E-100) (F-200) (G-200) (A-200) (B-100) (C-200)

ARTICLE REFERENCES

Equal Temperament (2013). In Encyclopædia Britannica. Retrieved from http://www.britannica.com/EBchecked/topic/190596/equal-temperament

Tuning Systems (2013). Retrieved from http://cnx.org/content/m11639/latest/